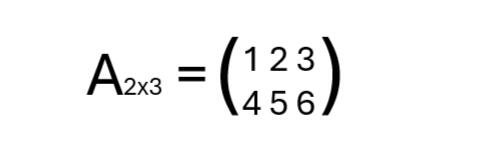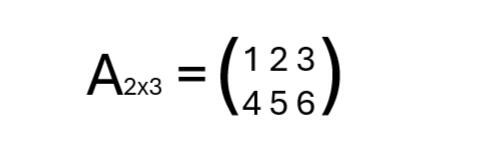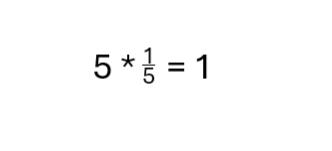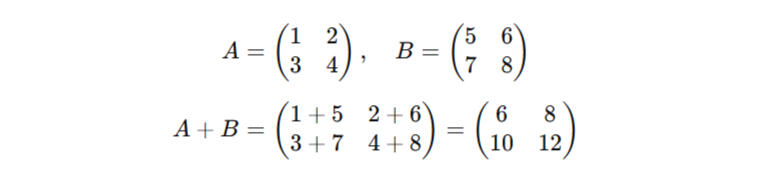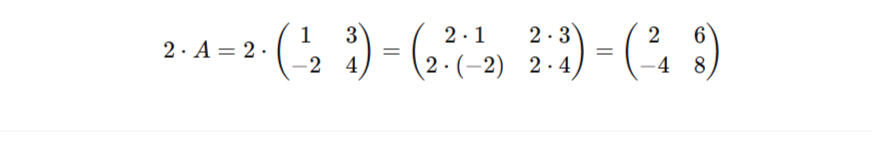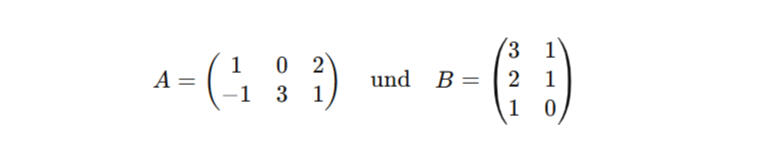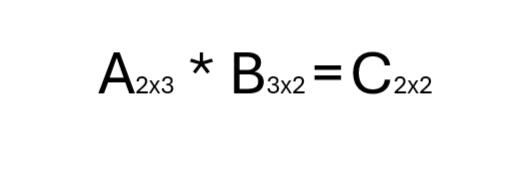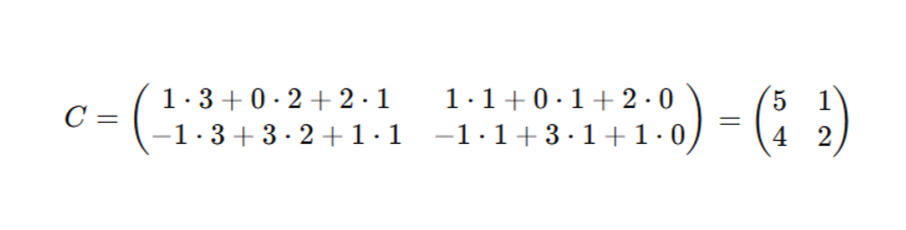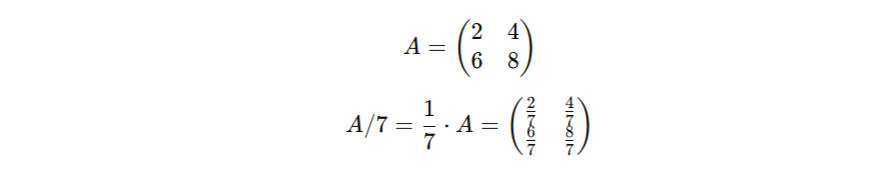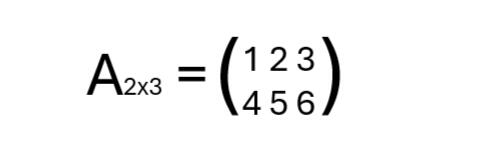FH-Westküste: Mathe Hilfsseite

Inhalt
Kurven Verschieben
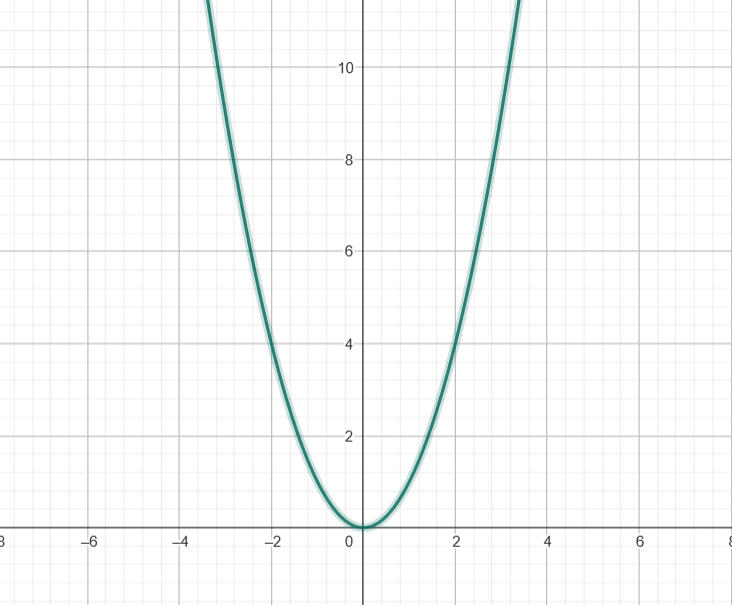
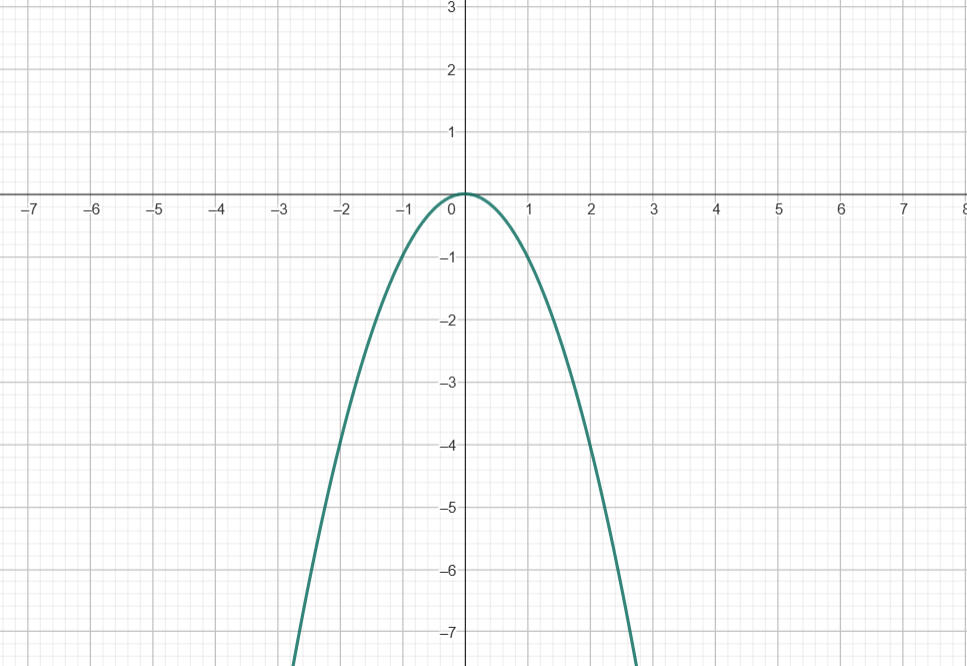
Schauen wir uns den den Fall einer Funktion f(x) = x² an. Diese beschreibt offensichtlich eine Normalparabel mit dem Scheitelpunkt (0|0) und sieht folgendermaßen aus:
Kurven Verschieben
Schauen wir uns den den Fall einer Funktion f(x) = x² an. Diese beschreibt offensichtlich eine Normalparabel mit dem Scheitelpunkt (0|0) und sieht folgendermaßen aus:
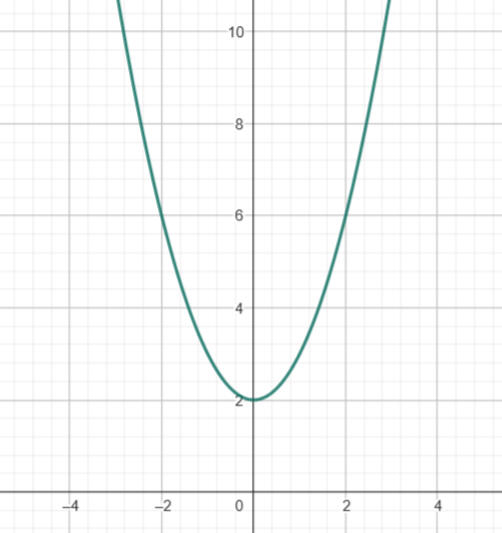
Die Funktion kann nun durch eine Konstante wie eine +2 erweitert werden. Hierbei gibt es zwei verschiedene Möglichkeiten wo diese nun Platziert werden kann, welche sich unterschiedlich auf die Kurve auswirken.
f(x) = x² +2
Hierbei wird die +2 als Konstanter Term zur Funktion hinzu gefügt. Dies bewirkt, dass die Gesamte Funktion an jedem Punkt unabhängig
vom x um 2 Punkte steigt.
Siehe:
f(4) = 4² = 16
f(4) = 4² + 2 = 18
Diese Regel gilt für jede Funktion und beide Vorzeichen, es gilt sich also zu Merken:
Wenn die Funktion f(x) einen Faktor +/- hat welcher kein x hat wird die Funktion um diesen Wert nach oben/unten verschoben.
Reden wir über Matrizen. Matrizen sind Rechteckige anordnungen von Zahlen und ggf. auch anderen Symbolen in Zeilen und Spalten, die in einer Klammer angegeben werden. Folgende Eigenschaften zeichnen sie aus.– Matrizen werden wie Funktionen mit Buchstaben benannt, zu differenzierung werden für Matrizen in der Regel Großbuchstaben verwendet. In Formeln oder Regelungen wird oftmals das A genutzt um eine Matrix zu beschreiben.– Eine Matrix besteht aus Zeilen und Spalten und die Anzahl beider ist von hoher Bedeutung für das Rechnen mit Matrizen. Dargestellt wird die Dimension wie folgt: Zeilen x Spalten
Das x wird hier als "Kreuz" ausgesprochen. Die Darstellung einer Matrix der reellen Zahlen mit 2 Zeilen und 3 Spalten wäre somit: A∈R2×3 oder A2x3
Wobei man bei der Kurzen Form die Zeichen eher nach unten stellt um Verwirrung zu vermeiden.
Eine solche Matrix könnte so aussehen:
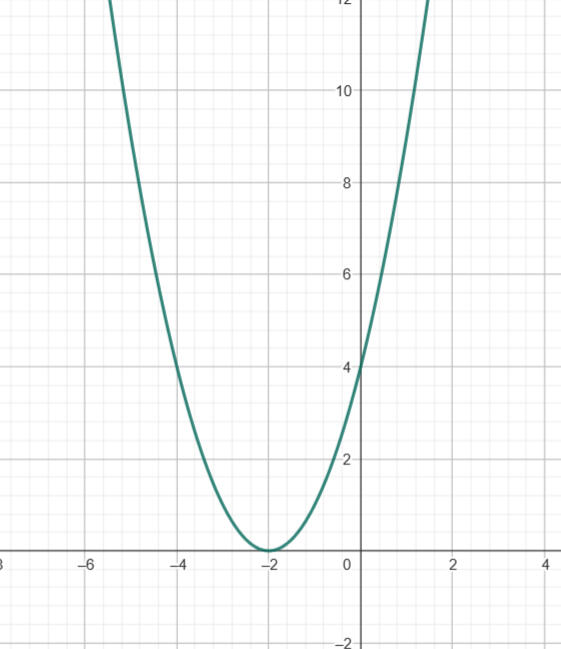
f(x) = (x+2)²
In diesem fungiert die +2 als konstante Verschiebung des x Wertes. Dies bewirkt, dass die Gesamte Funktion an jedem Punkt mit einem um 2 höheren Wert gerechnet wird. Damit nun der Y Wert 0 erreicht werden kann muss der eigentliche X-Wert um den gleichen Faktor geringer sein.
Siehe:
f(0) = 0² = 0
f(0) = (0+2)² = 4
f(-2) = ((-2)+2)² = 0
Aus diesem Grund sind nun alle Punkte der Kurve um den Faktor (hier 2) nach links verschoben also entgegen des Vorzeichens. Wäre das Vorzeichen also negativ (z.B. -2) müssten die x entsprechend höher sein und die Kurve würde nach Rechts wandern. Somit lässt sich merken:
Wenn bei der Funktion f(x) das x direkt um einen Konstanten Faktor erhöht/vermindert wird, verschiebt sich die Kurve entgegen dem Vorzeichen nach links/rechts.
Matrizen
Reden wir über Matrizen. Matrizen sind Rechteckige anordnungen von Zahlen und ggf. auch anderen Symbolen in Zeilen und Spalten, die in einer Klammer angegeben werden. Folgende Eigenschaften zeichnen sie aus.– Matrizen werden wie Funktionen mit Buchstaben benannt, zu differenzierung werden für Matrizen in der Regel Großbuchstaben verwendet. In Formeln oder Regelungen wird oftmals das A genutzt um eine Matrix zu beschreiben.– Eine Matrix besteht aus Zeilen und Spalten und die Anzahl beider ist von hoher Bedeutung für das Rechnen mit Matrizen. Dargestellt wird die Dimension wie folgt: Zeilen x Spalten
Das x wird hier als "Kreuz" ausgesprochen. Die Darstellung einer Matrix der reellen Zahlen mit 2 Zeilen und 3 Spalten wäre somit: A∈R2×3 oder A2x3
Wobei man bei der Kurzen Form die Zeichen eher nach unten stellt um Verwirrung zu vermeiden.
Eine solche Matrix könnte so aussehen:
– Ihnen sind Vielleicht Vektoren ein Begriff. Hierbei handelt es sich tatsächlich ebenfalls um Matrizen. Genauer ist ein Vektor eine Spezialform von Matrizen, welche nur eine Spalte haben.v = A∈R3x1– Es gibt mehrere Wege wie Matrizen verrechnet werden können– Es gibt mehrere Sonderformen der von Matrizen zwei davon sollen hier einmal Vorgestellt werden.
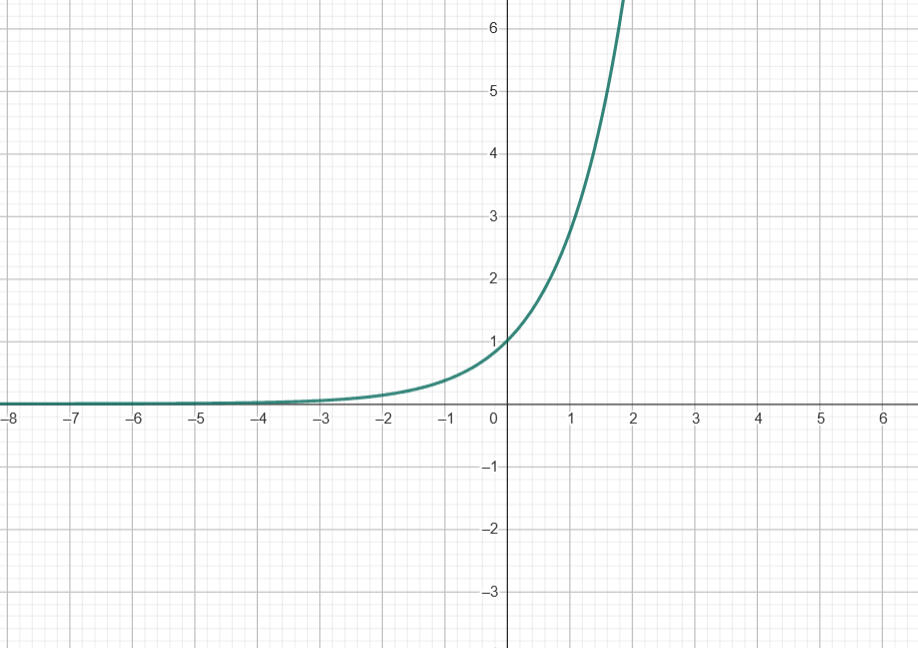
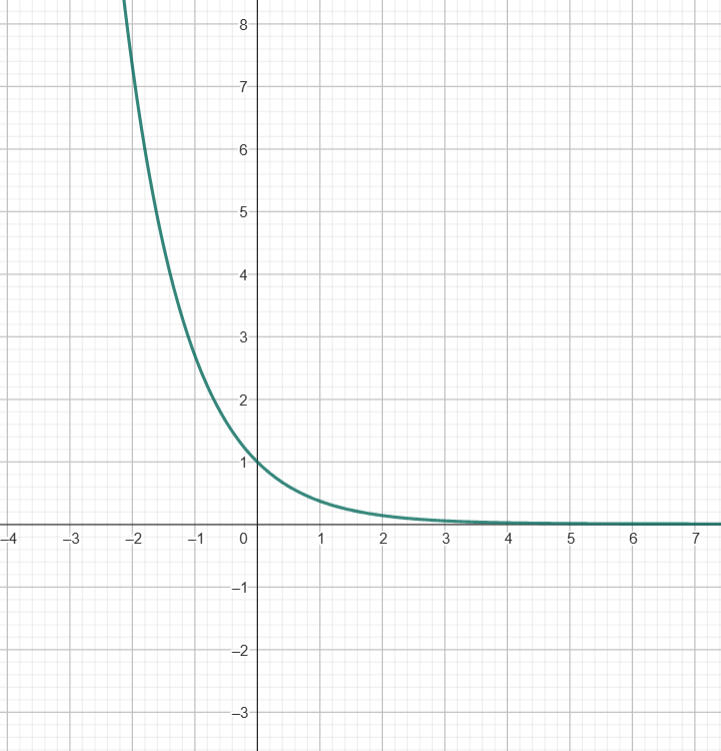
Eine weitere Möglichkeit die Funktion zu beeinflussen stellt ein Vorzeichen dar. Standartmäßig ist x² positiv kann jedoch auch negativ werden wenn wir ein - vor es setzen. Auch hier gibt es die Möglichkeit das x direkt oder die gesamte Funktion zu ergänzen. Da sich die Funktion x² für einen der Fälle nicht eignet wird das zweite Beispiel eine genauso ikonische Funktion nutzen ex. Diese sieht zur Erinnerung folgendermaßen aus:
f(x) = -x² | g(x) = -ex
Hierbei wird einfach das Vorzeichen negativ gesetzt. Der Effekt ist, recht offensichtlich, dass alle Ergebnisse nun das jeweils andere Vorzeichen haben, in diesem Fall ist somit nun alles negativ. Lediglich die Punkte, welche direkt auf der X-Achse liegen bleiben gleich, da um sie herum gespiegelt wird.
Siehe:
f(4) = 4² = 16
f(4) = -4² = -16
Es gilt sich also zu Merken:
Wenn die Funktion f(x) ein negatives Vorzeichen hat, wird diese an der X-Achse gespiegelt, womit alle Ergebnisse nun das jeweils andere Vorzeichen haben.
f(x) = (-x)² | g(x) = e-x
Dieser Fall sieht zwar ähnlich aus, ist aber ein anderer. Hier wird nämlich beim X-Wert vor der Verrechnung das Vorzeichen getauscht. Dies hat den Effekt, das bei allen X-Werten das Ergebnis nun das ist, was es beim jeweils anderen Vorzeichen wäre. Lediglich die Punkte, welche direkt auf der Y-Achse liegen bleiben gleich, da um sie herum gespiegelt wird.
Siehe:
f(2) = e² = 7,39
f(-2) = e-(2) = 0,14
f(2) = e-² = 0,14
f(-2) = e-(-2) = 7,39
Somit lässt sich merken:
Wenn bei der Funktion f(x) das x ein negatives Vorzeichen hat, wird diese an der Y-Achse gespiegelt, womit alle X-Werte nun das Ergebnis des jeweils anderen Vorzeichen haben.
Schauen wir uns nun ein Beispiel einer Funktion an welche verändert wurde:
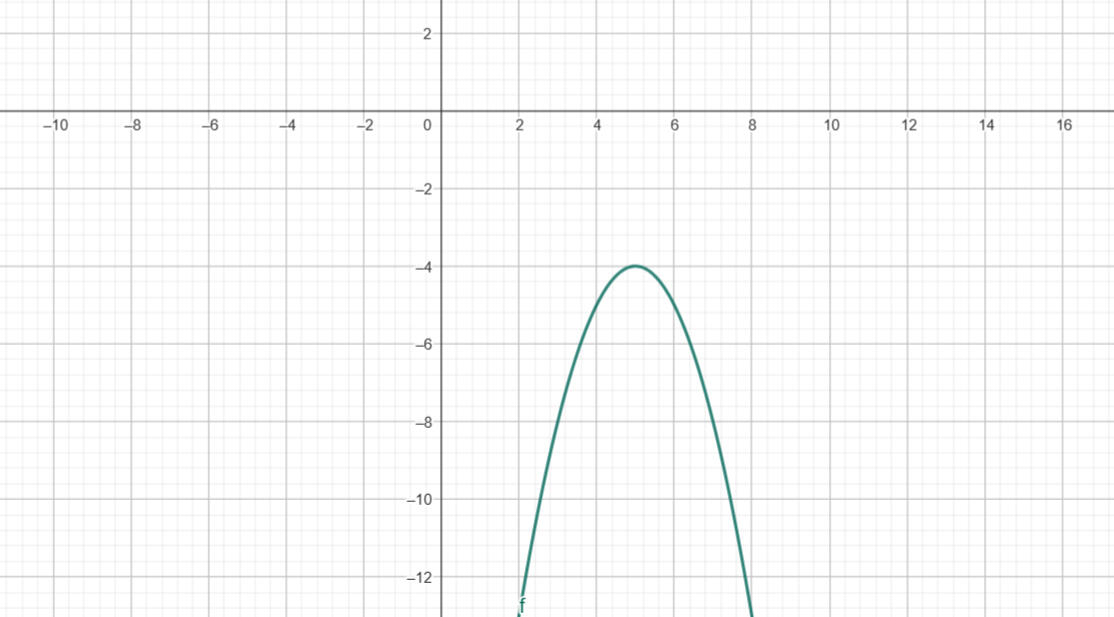
f(x) = -(-x + 5)2 - 4
Versuche diese allein Aufzuschlüsseln und zu zeichenen!
Die Funktion sieht so aus!
Obwohl diese Funktion auf den ersten Blick kompliziert aussieht kann man sie recht leicht entschlüsseln. Denkt man sich alle Vorzeichen und Konstanten weg erkennt man im Kern die Formel x². Man sieht nun das diese durch vier Konstanten beeinflusst wird.
1.
Der gesamte Term mit x wird durch ein - im Vorzeichen gedreht. Dadurch wird die Funktion an der X-Achse gespiegelt und ist nun nach unten geöffnet.
2.
Das x wird direkt durch eine +5 beeinflusst. Damit wird die ganze Funktion horizontal Verschoben. Sie wird nach links verschoben, da das Vorzeichen der 5 ein + ist.
3.
Der X-Wert wird ebenfalls durch ein - gedreht. Hierdurch wird die gesamte Funktion an der Y-Achse gedreht und ist nun rechts von der Abzisse (Y-Achse).
Tatsächlich könnte das innere von (-x+5) auf (x-5) geändert werden, da diese beiden Schreibweisen identisch sind. Das heißt dies hätte auch als einzelner Schritt gemacht werden können, in dem nach rechts verschoben wird. Es wäre sogar besser diese Schritte zusammen zu fassen, da man bei getrennten Schritten darauf achten muss zuerst zu verschieben und dann zu spiegeln. Die Form (x-5) ist somit eigentlich richtiger.
4.
Hinten wird die Konstante -4 hinzugefügt. Das heißt die gesamte Funktion wird um 4 Einheiten nach unten geschoben.
Matrizen
Reden wir über Matrizen. Matrizen sind Rechteckige anordnungen von Zahlen und ggf. auch anderen Symbolen in Zeilen und Spalten, die in einer Klammer angegeben werden. Folgende Eigenschaften zeichnen sie aus.– Matrizen werden wie Funktionen mit Buchstaben benannt, zu differenzierung werden für Matrizen in der Regel Großbuchstaben verwendet. In Formeln oder Regelungen wird oftmals das A genutzt um eine Matrix zu beschreiben.– Eine Matrix besteht aus Zeilen und Spalten und die Anzahl beider ist von hoher Bedeutung für das Rechnen mit Matrizen. Dargestellt wird die Dimension wie folgt: Zeilen x Spalten
Das x wird hier als "Kreuz" ausgesprochen. Die Darstellung einer Matrix der reellen Zahlen mit 2 Zeilen und 3 Spalten wäre somit: A∈R2×3 oder A2x3
Wobei man bei der Kurzen Form die Zeichen eher nach unten stellt um Verwirrung zu vermeiden.
Eine solche Matrix könnte so aussehen:
Sonderformen
Bei den ganzen verschiedene Möglichkeiten von Matrizen gibt es auch einige Formen welche einzigartige Eigenschaften besitzen und als Sonderformen betrachtet werden.– Ihnen sind Vielleicht Vektoren ein Begriff. Hierbei handelt es sich tatsächlich ebenfalls um Matrizen. Genauer ist ein Vektor eine Spezialform von Matrizen, welche nur eine Spalte haben.v = A∈R3x1– In der Mathematik gibt es das Konzept des neutralen Elements. Hierbei handelt es sich um eine Element, das bei einer bestimmten Verknüpfung dafür sorgt, das das Ergebnis unverändert bleibt. Dieses unterscheidet sich je nach Verknüpfung und beschreibt unter anderem folgende:Addition: 16 + 0 = 16
Subtraktion: 16 - 0 = 16
Multiplikation: 16 * 1 = 16
Division: 16 / 1 = 16Für Matrizen gibt es ein solches Element ebenfalls, die Sogenannte Einheitsmatrix. Diese wird mit einem I bezeichnet und ist wie folgt definiert:
A * I = I * A = A
Somit wird bei einer Verrechnung mit der Matrix die Ursprungsmatrix nicht verändert. Aufgebaut ist die Einheitsmatrix als Quadratische Matrix und funktioniert auch nur mit diesen. Dabei ist die Diagonale von oben links bis unten rechts mit 1 versehen während die anderen Werte 0 sind.– Bei dieser Form muss man etwas ausholen. Es gibt in der Mathematik das Konzept der inversen. Hierbei handelt es sich um das Gegenstück für einen Wert der den eigentlichen Wert Aufhebt. Das Ergebnis dieser Rechnung ist dann das neutrale Element, welches die restliche Rechnung nicht mehr beeinflusst. Für die 5 wäre es also folgendes.
Der Bruch 1/5 ist also die inverse zu der Zahl 5. Genutzt wird dies zb. beim Lösen von Gleichungen bei der man den Wert 5 herausrechnen kann indem man ihn durch 5 Teilt um ihn weg zu bekommen. Genaugenommen Teilt man dabei eben nicht durch 5 sondern multipliziert die inverse 1/5. Auch verschwindet der Wert hier nicht sondern er wird zur 1 dem neutralen Element wodurch er quasi weg ist.Bei den Matrizen gibt es ebenfalls eine inverse bekannt als die Inverse Matrix A-1. Für die gilt:A * A-1 = A-1 * A = IDass heißt man kann die Inverse A-1 einer Matrix A auf beiden Seiten mit dieser Multiplizieren um die Einheitsmatrix zu erhalten. Zu beachten ist, das diese inverse jedoch ausschließlich für Quadratische Matrizen definiert ist und somit nicht bei allen möglich ist.
Rechenregeln
Wie normale Zahlen auch können Matrizen mit den verschiedenen Operatoren (+,- etc.) verrechnet werden. Es gibt jedoch einige Dinge zu beachten:+/- Matrizen können Addiert und subtrahiert werden. Hierbei werden alle Elemente auf der gleichen Position addiert/subtrahiert. Hierfür müssen die Matrizen die exakt gleichen Dimensionen besitzen, das heißt eine 2x2 Matrix kann nur mit einer anderen 2x2 Matrix addiert/subtrahiert werden. Eine addition/subtraktion einer Matrix mit einer einzelnen Zahl ist jedoch nicht möglich, nur mit anderen Matrizen.
Multiplikation Matrizen können entweder mit einer Zahl oder einer anderen Matrix multipliziert werden.– Die Multiplikation mit einer Zahl ist Simpel, hierbei werden lediglich alle Elemente der Matrix mit der Zahl Multipliziert.
– Die Multiplikation zweier Matrizen ist etwas Anspruchsvoller, da nicht alle Matrizen miteinander multipliziert werden können. Genauer werden bei einer Multiplikation die Spalten der ersten Matrix, mit den Zeilen der zweiten Multipliziert. Aus diesem Grund müssen diese auch gleich sein, während der jeweils andere Wert tatsächlich egal ist. Das heißt für die Folgenden Beispiele:
– Im ersten Fall ist eine Multiplikation möglich, da die jeweiligen inneren Abmessungen zusammenpassen, auch wenn die äußeren völlig unterschiedlich sind.
– Im zweiten Fall wiederum sind die Matrizen sogar gleichgroß, da aber die inneren nicht zusammen passen, können sie nicht multipliziert werden.– Um sich schnell einen Eindruck darüber zu machen ob man zwei Matrizen verrechnen kann, kann es also hilfreich sein, die Dimension immer dazu zu schreiben.Nehmen wir nun an wir haben folgende Matrizen gegeben und wollen diese Multiplizieren:
– Hier ist es nun wichtig zu beachten wie rum gerechnet wird. In diesem Fall wären tatsächlich beide Kombinationen möglich, da die Spalten und Zeilen invertiert sind. Wird nun diese Folge gewählt, stehen die 3 in der Mitte und stimmen überein, somit können sie Multipliziert werden.
Was nun zu sehen ist, wird die entstehende Matrix die außenstehenden Dimensionen habe, die nicht bei der berechnung "verbraucht" wurden. Wenn man sich das Merkt weiß man auch direkt, wie die Ergebnismatrix aussehen wird.
– Um das nun zu Rechnen muss man die erste Spalter der ersten und die erste Zeile der zweiten Matrix wählen. Man verrechnet nun die Elemente die an der gleichen stelle stehen um so auf die Folgende Rechnung zu kommen:
Division Die Division ist etwas komplizierter, da sie Grundsätzlich bei Matrizen nicht möglich bzw. nicht definiert ist.– Während die Schreibweise, bei der man eine Matrize durch einen Wert Teilt technisch nicht korrekt bzw. definiert ist, kann man Matrizen trotzdem mit einem Trick durch einen Wert Teilen. Hierzu muss man sich nur klar werden das, das Teilen eines Wertes das gleiche ist wie ihn mit einem Bruch zu multiplizieren, der das neutrale Element 1 im Zähler und den zu teilenden Wert im Nenner hat.
– Die Division zweier Matrizen ist ebenfalls nicht definiert kann jedoch erneut durch einen Trick erreicht werden, wenngleich dieser einen nicht unwesentlichen Aufwand erfordert. Hierzu wird die bereits Vorgestellte inverse Matrix A-1 benötigt. Wie oben beschrieben stellt die inverse des Wertes 5 den Bruch 1/5 dar, welcher dem Teilen durch 5 entspricht. Genauso ist die Multiplikation mit der inversen von A das gleiche wie das Teilen durch A. Es ist definiert:B/A (nicht definiert) -> A-1 * B
Matrizen
Reden wir über Matrizen. Matrizen sind Rechteckige anordnungen von Zahlen und ggf. auch anderen Symbolen in Zeilen und Spalten, die in einer Klammer angegeben werden. Folgende Eigenschaften zeichnen sie aus.– Matrizen werden wie Funktionen mit Buchstaben benannt, zu differenzierung werden für Matrizen in der Regel Großbuchstaben verwendet. In Formeln oder Regelungen wird oftmals das A genutzt um eine Matrix zu beschreiben.– Eine Matrix besteht aus Zeilen und Spalten und die Anzahl beider ist von hoher Bedeutung für das Rechnen mit Matrizen. Dargestellt wird die Dimension wie folgt: Zeilen x Spalten
Das x wird hier als "Kreuz" ausgesprochen. Die Darstellung einer Matrix der reellen Zahlen mit 2 Zeilen und 3 Spalten wäre somit: A∈R2×3 oder A2x3
Wobei man bei der Kurzen Form die Zeichen eher nach unten stellt um Verwirrung zu vermeiden.
Eine solche Matrix könnte so aussehen:
Gleichungssysteme
Bei Gleichungssystemen handelt es sich um Systeme die aus Mehreren Gleichungen bestehen. Zur Erinnerung eine Gleichung besteht aus einem Gleichheitszeichen = und auf beiden Seiten von diesem muss etwas stehen, das sich entspricht also gleich ist. In der Regel ist auf der rechte Seite ein Werte und auf der linken mindestens eine unbekannte Variable, die durch das Auflösen der Gleichung gefunden werden kann. Eine Gleichung könnte beispielsweise so aussehen und gelöst werden:2x + 3 = 7
2x = 7 - 3
2x = 4
x = 4/2
x=2Dieser Fall war nun relativ einfach, wenn eine Gleichung jedoch mehrere Unbekannte beinhaltet, ist diese Methode nicht mehr möglich.2x + 3y = 12Um diese lösen zu können bedarf es einem Gleichungssystem, das heißt es wird zunächst eine weitere Gleichung für jede unbekannte benötigt, bei welchen die Werte für x,y und z auch die gleichen sind.2x + 3y = 12
3x + 6y = 21Jetzt kann man einige von mehreren Methoden nutzen um dieses Gleichungssystem zu lösen. Im folgenden werden 3 Methoden vorgestellt.
Einsetzungsverfahren
Bei diesem Verfahren wir die eine Gleichung in die andere eingesetzt. Hierfür muss diese zunächst nach einer der Variablen umgestellt werden, sodass diese alleine auf einer Seite steht. Damit hat man ermittelt, was dieser Variable entspricht und kann diese in der anderen Gleichung durch diesen Term ersetzen. Der entstehende Term ist in der Regel komplizierter, aber umfasst nun nur noch eine Variabel und kann Normal aufgelöste werden. Diese Methode ist auch mit größeren Gleichungssystemen möglich, wird jedoch bereits bei 3 Variablen sehr kompliziert sodass sich hier auf ein Beispiel mit zwei Variablen beschränkt wird.
Hier ein Beispiel:x + 3y = 9
3x + 2y = 13Wir entscheiden uns die erste Gleichung in die zweite einzusetzen und stellen sie dafür nach x um.x + 3y = 9
x = 9 - 3yJetzt ist bekannt, was x entspricht, womit wir das x in der zweiten Gleichung entsprechend ersetzen können.3x + 2y = 13
3*(9 - 3y) + 2y = 13
27 - 9y + 2y = 13
27 - 7y = 13
-7y = -14
7y = 14
y = 2Nun ist uns y bekannt und der Wert kann in eine Gleichung eingesetzt werden. Praktischerweise haben wir bereits eine wo direkt das x als Ergebnis rauskommt.x = 9 - 3y
x = 9 - 3 * 2
x = 9 - 6
x = 3Num haben wir beide Unbekannte bestimmt.Additions/Subtraktionsverfahren
Gleichsetzungsverfahren
Matrixverfahren
Dieses Verfahren ist auch als Gauß-Algorithmus bekannt.
Additions/Subtraktionsverfahren
Der Gedanke dieses Verfahrens ist, das man Gleichungen auch Addieren bzw. Subtrahieren kann, da wenn die Einzelteile Addiert werden auch die Summe addiert werden kann, wenn diese sich aus den gleichen Faktoren ergibt.Um den Gedanken verständlicher zu gestalten muss man sich zwei Tische vorstellen. Auf einem liegen 3 Äpfel (mit Gewicht x) und 2 Birnen (mit Gewicht y) und damit eine Summe von Beispielsweise 7kg. Auf einem anderen liegen 2 Äpfel und eine Birne und damit 4kg. Da die Faktoren gleich sind, kann man diese Tische zusammenfassen um so 5 Äpfel und 3 Birnen zu bekommen und eine Summe von 11kg zu erhalten.In diesem Verfahren werden nun die Gleichungen addiert/subtrahiert um dabei einen oder mehrere Faktoren auf null zu bekommen. Das sieht folgendermaßen aus:2x + 3y = 12
3x + 6y = 21Zunächst müsse die Werte so verändert werden, das eine der Variablen gleich ist. Dafür nehmen wir die erste Gleichung mal -2.2x + 3y = 12 | *(-2)
-4x - 6y = -24Das y hat nun den gleichen Wert wie in der anderen Gleichung nur negativ, wir können diese also nun addieren.(3x + 6y = 21) + (-4x - 6y = -24)
3x - 4x + 6y - 6y = 21 - 24
-x = -3
x = 3Die Gleichung die bleibt kann nun einfach Aufgelöst werden um den Wert für x zu ermitteln. Dieser kann jetzt wider in eine der Ursprungsgleichungen eingesetzt werden um den Wert für y zu erhalten.2x + 3y = 12
2 * 3 + 3y = 12
6 + 3y = 12
3y = 12 - 6
3y = 6
y = 6/3
y = 3
Gleichsetzungsverfahren
Bei diesem Verfahren werden beide Gleichungen so umgestellt, das sie den Gleichen Wert auf einer Seite der Gleichung besitzen, in der Regel eine der Variablen. Da die jeweils andere Seite das Gleiche Ergebnis zeigt, können diese dann Gleichgesetzt werden. Hier ein Beispiel:5x - 9y = 7
8x + y = 42Um diese gleich zu setzen können wir jetzt nach x oder y Auflösen, wir wählen x.5x - 9y = 7
5x = 7 + 9y
x = (7 + 9y)/5
8x + y = 42
8x = 42 - y
x = (42 - y)/8Wir haben jetzt zwei Gleichungen, die beide den Wert x Ergeben. Das bedeutet, das beide das gleiche Ergebnis haben und mit einem = kombiniert werden können, also Gleichgesetzt werden.(7 + 9y)/5 = (42 - y)/8Jetzt gilt es diese nach y Aufzulösen, hierfür müssen zunächst die Brüche entfernt werden, indem man mit den entsprechenden Werten Multipliziert.(7 + 9y)/5 = (42 - y)/8 | *5
(7 + 9y) = 5 * (42 - y)/8 | *8
8 * (7 + 9y) = 5 * (42 - y)Nun die Klammern Auflösen.8 * (7 + 9y) = 5 * (42 - y)
8 * 7 + 8 * 9y = 5 * 42 - 5 * y
56 + 72y = 210 - 5yUnd jetzt lässt sich einfach nach y Auflösen.56 + 72y = 210 - 5y
56 + 72y + 5y = 210
72y + 5y = 210 - 56
77y = 154
77y/77 = 154/77
y = 2Mit dem y Ermittelt, lässt sich nun auch das x Bestimmen, wieder durch Einsetzen in eine Gleichung.8x + y = 42
8x + 2 = 42
8x = 40
x = 40/8
x = 5